How to Read the Residual Plots in R

In a previous blog mail, I described how to apply a spread plot to compare the distributions of several variables. Each spread plot is a graph of centered information values plotted against the estimated cumulative probability. Thus, spread plots are similar to a (rotated) plot of the empirical cumulative distribution function. Users of the SAS regression procedures will recognize the spread plots as one of the plots that are created automatically by procedures such equally PROC REG. The spread plots of the fitted and residual values announced in the eye cavalcade of the 3rd row of the regression diagnostics panel.

In the SAS documentation, the balance-fit spread plot is also called an "RF plot." This article describes how to interpret the R-F spread plot.

The residual-fit spread plot in SAS output

When I commencement saw the R-F spread plot in the PROC REG diagnostics panel, there were two things that I establish confusing:

• The title of the left plot is "Fit–Hateful." I read the title as "fit hyphen mean," and I didn't know what that meant. However, the correct manner to read the title is "fit minus hateful," which is equivalent to "centered fit."
• The label for the horizontal axis is "Proportion Less." I didn't know what that meant, either. I now know that scatter plot shows empirical quantiles versus their plotting positions. Recall that the pthursday empirical quantile is the data value that is greater than (or equal to) a proportion p of the information values. Therefore, if a point on the scatter plot has coordinates (p_i, q_i ), it means that the vertical coordinate is the ith quantile, and approximately p_i of the other data values are less than that proportion.

History of the residual-fit spread plot

The spread plot is a graph of the centered data versus the corresponding plotting position. Essentially, information technology is a plot of the sorted data against the corresponding rank, except that using the plotting position instead of ranks makes information technology possible to compare variables that have different numbers of nonmissing observations. As well, using centered data instead of raw values enables you to compare the spread of variables that have unlike means.

William S. Cleveland featured the residual-fit spread plot in his book Visualizing Data (1993). He describes how to create a quantile plot on pp. 17–20, and describes quantile plots for fitted and residual values on p. 35–38. Then he says (p. twoscore):

It is informative to report how influential the [explanatory]variable is in explaining the variation in the [response variable]. The fitted values and the residuals are two sets of values each of which has a distribution. If the spread of the fitted-value distribution is large compared with the spread of the residual distribution, then the [explanatory]variable is influential. If information technology is small-scale, the [explanatory]variable is not as influential.... Since it is the spreads of the distributions that are of interest, the fitted values minus their overall mean are graphed.... This residuum-fit spread plot, or r-f spread plot, shows [whether]the spreads of the residuals and fit values are comparable.

Cleveland goes on to use the R-F spread plot virtually 20 times in multiple examples.

The residual-fit spread plot as a regression diagnostic

Following Cleveland'south examples, the residual-fit spread plot can be used to assess the fit of a regression as follows:

• Compare the spread of the fit to the spread of the residuals. This is the main idea. If the left side of the plot (the centered fitted values) is taller than the right side (the balance values), then you conclude that the spread of the balance values is small relative to the spread of the fitted values.
• Examine the distribution of the balance values. The quantile plot of the residual values contains all of the information that a box plot does—and more than. If the distribution does not appear to be commonly distributed, the model might not fit the data.
• Are there extreme values for the distribution of the residual values? These indicate outliers: observations for which the observed value is far from the fitted value.
• Are at that place farthermost values for the distribution of the fitted values? These might indicate influential observations that have high leverage in the model. They need to be investigated.

Some examples on imitation data

The all-time mode to practice interpreting the R-F spread plots are to view some examples for which the true model is known. The post-obit Data step simulates two response variables:

              data              RegData(              drop=i);              call              streaminit(              12345              );              do              i =              1              to              100;              x              = rand(              "Normal"              );    y1 =              2              +              iv              *x    + rand("Normal", 0, 0.25);              /* small error */              y2 =              two              +              4              *x**ii + rand("Normal", 0, 1);              /* not linear in x */              output;              finish;              run;

For a real regression analysis, I would look at several diagnostic plots, but in the subsequent examples I will only interpret the residual-fit spread plots. I utilize the DIAGNOSTICS(UNPACK) pick on the PLOTS= option to extract the R-F spread plot from the diagnostics panel.

Example 1: Examining the balance variation in a model

The y1 variable has a pocket-sized error term. The following statements display the R-F spread plot:

              title              "y = 2 + four*ten + eps, eps ~ N(0,0.25)"; ods              select              RFPlot;              proc reg              information              = RegData plots=diagnostics(unpack);    model y1 =              x;              quit;

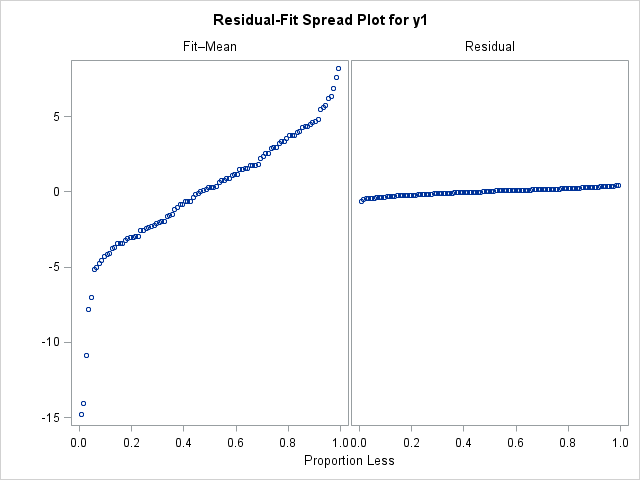
Notice that the left plot (the centered fitted values) is "taller" than the right plot (the remainder values), which indicates that the residual values have a smaller spread. In terms of the model, the 10 variable accounts for a significant portion of the variation in the model, with only a petty residual variation.

You can modify the standard departure of the fault term to five and rerun the plan. The new R-F spread plot (not shown), shows that the spread of the residue values is larger than the spread of the fitted values. The estimation would exist that considerable variation remains later on accounting for the upshot of the x variable.

Instance ii: A misspecified model

In the previous example, the model was correctly specified. In this second example, the truthful model is quadratic in the x variable, only the fitted model is linear in x.

              title              "y = 2 + four*ten**3 + eps, eps ~ N(0,0.25)"; title2              "Model is y = x"; ods              select              RFPlot;              proc reg              data              = RegData plots(only)=diagnostics(unpack);    model y2 =              x;              quit;

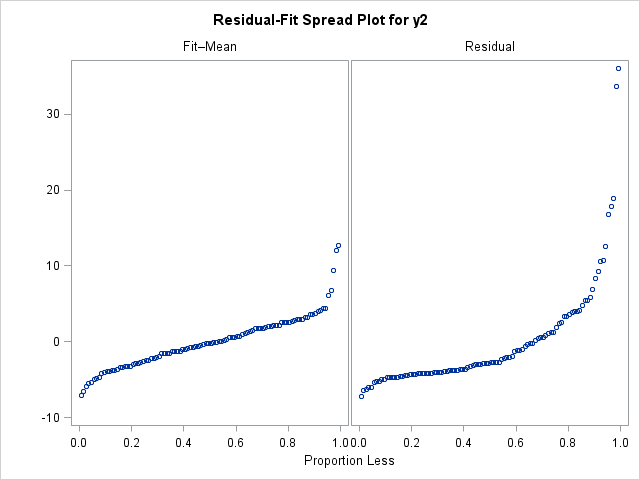
In the R-F spread plot for the (misspecified) model, the right-paw plot is taller than the left-manus plot. This shows that there is a lot of variation that is not explained by the model. Furthermore, the residuum distribution does not appear to exist normally distributed. The right tail of the rest distribution is long, and the distribution is skewed. If I saw a plot like this in real data, I would expect at other plots (such as the plot of residuals versus the predicted values) to see if the residuals exhibit a pattern that can be modeled.

Closing Comments

Several SAS regression procedures produce a regression diagnostics panel automatically. Each graph reveals information about the regression model and whether it fits the data well. This article has described how to interpret a residue-fit plot, which is located in the concluding row of the diagnostics panel. The residual-fit spread plot, which was featured prominently in Cleveland's book, Visualizing Data, is 1 tool in the arsenal of regression diagnostic plots.

How to Read the Residual Plots in R

Source: https://blogs.sas.com/content/iml/2013/06/12/interpret-residual-fit-spread-plot.html

Share this post